Supón que tienes un cuerpo que rueda por un acantilado con una velocidad de 5 m/s. El cuerpo golpea el suelo a una distancia d de la base de un acantilado que tiene una altura de 30 m. La figura 3 muestra el movimiento del proyectil sin ángulo, es decir, lanzado paralelo a la horizontal. Calcula el alcance d recorrido por el objeto.

Figura 3. Movimiento del proyectil sin ángulo. Movimiento del proyectil sin ángulo. Usama Adeel - StudySmarter Originals
Solución
Para calcular d, la distancia desde la base del acantilado, necesitamos comprender mejor el movimiento en las direcciones x e y.
Suponiendo que no hay resistencia del aire y que sólo actúa sobre la bola la fuerza gravitatoria, la velocidad en la dirección x será de 5 m/s hasta que la bola toque el suelo. En la dirección y, la pelota tiene una aceleración constante de 9,81m/s2, provocada por la fuerza gravitatoria.
Pero, ¿cuál es la velocidad inicial en la dirección y?
Como ya se ha dicho, dado que el movimiento en las direcciones x e y son independientes entre sí, la velocidad de 5 m/s en la dirección x no influye en el movimiento en la dirección y. Por lo tanto, la bola rueda por el acantilado con una velocidad inicial de 0 m/s en la dirección y.
El desplazamiento horizontal será de -30 m porque la dirección descendente se considera negativa junto con la aceleración de caída libre, que es de -9,81 m/s2.
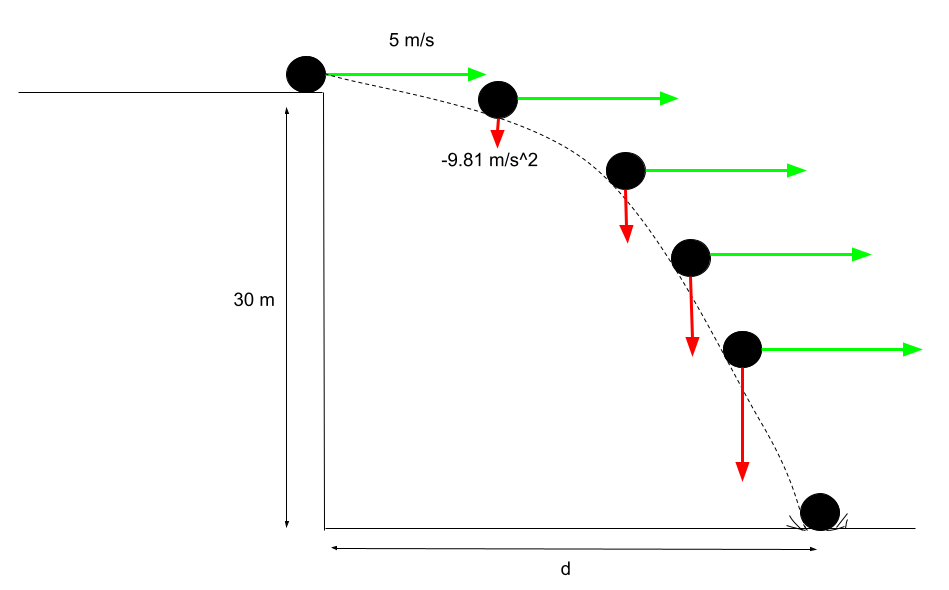
Figura 4. La velocidad en la dirección y aumentará debido a la aceleración en la dirección y. La velocidad en la dirección x permanecerá constante. Usama Adeel - StudySmarter Originals
Para la dirección x
Velocidad inicial: ux = 5 m/s
Distancia recorrida en la dirección x: dx = ?
Para la dirección y
Velocidad inicial: uy = 0 m/s
Desplazamiento:sy = -30 m
Aceleración debida a la caída libre =ay = -9,81 m/s2
A partir del movimiento en la dirección y, podemos calcular el tiempo t porque el tiempo es el mismo en la dirección x y en la dirección y. Utilizando la segunda ecuación del movimiento e introduciendo los valores, obtenemos
\[s_y = u_y \cdot t + \frac{1}{2} a \cdot t^2\].
\[-30 m = 0 \cdot t + \frac{1}{2} (9,81 m/s^2) \cdot t^2]
\cdot t = 2,47 s\]
Por tanto, el tiempo que tarda la pelota en llegar al suelo desde una altura de 30 m es de 2,47 s.
Para calcular la distancia recorrida desde la base del precipicio dx, volvemos a utilizar la segunda ecuación del movimiento, pero esta vez será para el movimiento en la dirección x.
\[d_x = u_x \cdot t + \frac{1}{2} a_x \cdot t^2\]
\[d_x =5 m/s \cdot (2,47 s) + \frac{1}{2} (0) \cdot (2,47s)^2\]
\d_x = 12,35 m\]
La distancia que recorre la pelota en la dirección x con una velocidad inicial de 5 m/s desde una altura de 30 m es de 12,35 m.
Puedes utilizar cualquier ecuación de movimiento para calcular una entidad concreta en función del problema relacionado con el movimiento de un proyectil.














