Cuando un dado se lanza, se sabe que la probabilidad de que salga uno de los seis posibles resultados es \(1/6\). Este resultado es la probabilidad. Pero, ¿cómo se distribuye esta probabilidad? Es decir, ¿cuánta probabilidad hay de que salga un uno o un seis? En un dado, esto es \(1/6\) cada uno; es decir, la probabilidad se distribuye equitativamente (es decir, en partes iguales). De manera muy primitiva, así es cómo se distribuye la probabilidad en el evento de lanzar un dado.
Pero, ¿qué pasa si hay muchos eventos? Y, ¿qué pasa si la probabilidad de que ocurra cada uno no es la misma, sino que cambia? En estos caso la probabilidad de que ocurra cada evento se distribuye entre todos los valores y no es igual en todos.
A una manera de representar esta distribución de un evento se le llama distribución de probabilidad y esta es una función muy importante.
Distribuciones de probabilidad
La distribuciones de probabilidad son funciones usadas en estadísticas, que te pueden decir cuán probable es obtener cierto resultado en un rango específico.
Por ejemplo, cuán probable es obtener que la altura de los alumnos de una clase caiga entre \([1{,}67\text{ m}; 1{,}74\text{ m}]\).
La función de probabilidad es parecida a una función de cálculo y análisis \(f(x)\), donde \(x\) es el valor del resultado y la función \(f(x)\) nos dice la probabilidad de que la variable que toma valores en un rango \([a, b]\) tome esos valores.
Hay dos tipos de distribuciones de probabilidad:
Funciones de distribución discretas: donde una variable aleatoria toma solo ciertos valores discretos.
Funciones de distribución continuas: donde una variable aleatoria toma cualquier valor en un intervalo \([a,b]\).
Una de las funciones más conocidas es la función de densidad de la distribución normal, la cual es:
\[{{1}\over{\sqrt[2]{2\pi}}} e^{{{-x^2}\over{2}}}\]
Función de distribución continua
Para calcular las probabilidades cuando tenemos una variable aleatoria continua, utilizamos lo que se llama la función de densidad. Para que una función \(f(x)\) sea una función de densidad de una variable aleatoria continua sobre la recta real, debe cumplir:
\(f(x)\geq 0\), para todo \(x\) en un rango \([a, b]\).
El área bajo la curva y por encima del eje de abscisas es igual a \(1\).
El rango \([a, b]\) delimita los valores que la variable puede tomar.
Debido a esto, la probabilidad de que el valor de una variable continua aleatoria \(X\) esté dentro de un intervalo \([a,b]\) es el área bajo la curva dentro de este intervalo:
\[P(a\leq X\leq b)=\int_a^b f(x)dx\]
Esto implica que la probabilidad de que una variable aleatoria tome un valor concreto es nulo, puesto que, por definición:
\[\int_a^af(x)dx=0\]
Ahora, si queremos calcular la probabilidad acumulada hasta el valor \(X=x\), utilizamos la función de distribución de la variable \(X\):
\[F(x)=P(X\leq x)=\int_{-\infty}^x f(x)dx\]
Por tanto, se verifica que la función de densidad sea la derivada de la función de distribución:
\[f(x)=F'(x)\]
Calcula la función de distribución de la siguiente función de densidad:
\[f(x)=\left\{\begin{align}\,&0\space\space\space x\in(-\infty,0)\\ &\dfrac{x}{2}\space\space\space x\in[0,2]\\ &0 \space\space\space x\in(2,+\infty) \end{align}\right.\]
Solución:
Para calcular la función de distribución, debes integrar la función de densidad, tal como se mencionó anteriormente. Como nuestra función de densidad empieza a tomar valores a partir del \(0\), este será el límite inferior de nuestro intervalo de integración (entre \(-\infty\) y \(0\) la función es nula):
\[F(X)=\int_{-\infty}^{+\infty}f(x)dx=\int_{0}^X f(x)dx=\int_0^X \dfrac{x}{2}dx=\dfrac{X^2}{4}\]
Por tanto, la función de distribución será:
\[F(X)=\left\{\begin{align}\,0\space\space\space X&\in(-\infty,0)\\ \dfrac{X^2}{4}\space\space\space X&\in[0,2]\\ 0 \space\space\space X&\in(2,+\infty) \end{align}\right.\]
A continuación, están representadas la función de densidad y la función de distribución.
Fig. 1.Función de densidad
Fig. 2: Función de distribución.
En general, la distribución normal es la distribución continua más usada; aparece en muchos experimentos que harás en tus laboratorios y clases de bachillerato. Sin embargo, hay otras distribuciones continuas como:
- Distribución Beta
- Distribución Gamma
- Distribución de Pareto
Algunas de estas aparecen en fenómenos como la altura de las olas en el mar, debido al viento que sopla sobre el océano.
La distribución normal: ejemplo
Hablaremos un poco de la distribución normal, aunque sea brevemente.
La distribución normal es la distribución que forma una campana alrededor del valor esperado.
Si quieres saber más en detalle de esta distribución consulta nuestro artículo Distribución normal.
Esta distribución es muy importante, ya que la dispersión de los datos (cuánto se alejan los datos del valor central) es regular. Al ser la dispersión regular, hay una valor que te permite saber entre cuál dato mayor y menor se encuentra el \(64,2%\) de los datos. Este valor se llama la desviación estándar, y su símbolo es \(\sigma\).
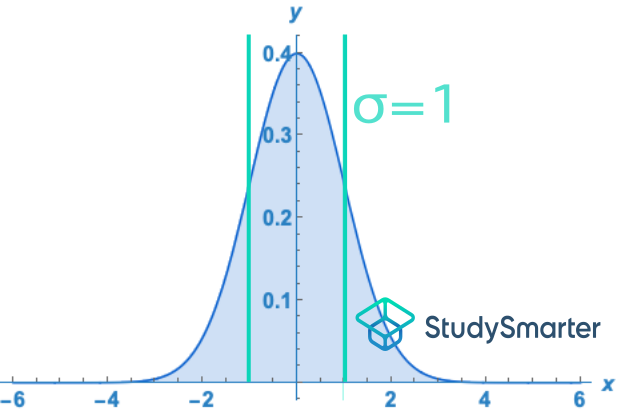
Fig. 3: Distribución normal y límites de la desviación estándar .
Si multiplicas el valor de \(\sigma\), obtenemos el valor mayor y menor, entre los cuales vive el \(95.8%\) de los datos; si lo multiplicas por tres, obtendrás el \(99.8%\) de los datos.
Hay dos valores importantes en las distribuciones continuas de probabilidad: la varianza y la esperanza.
Esperanza matemática
La probabilidad de que un número suceda en un experimento aleatorio no es independiente del resultado esperado. Como ya mencionamos, los valores cercanos al valor verdadero o esperado tendrán más probabilidad de salir.
Se conoce como esperanza matemática al producto de la probabilidad de un resultado por el valor esperado.
Esperanza matemática: fórmula
Como hemos dicho, podemos definir la esperanza matemática como:
\[\mu=E[X]=\int_{-\infty}^{+\infty}xf(x)dx\]
Calcula la esperanza matemática de la función de densidad del ejemplo anterior.
Solución:
Si tenemos la función de densidad \(f(x)\), calculamos su esperanza con la fórmula anterior:
\[\mu=\int_{-\infty}^{+\infty}xf(x)dx=\int_{0}^2 x\dfrac{x}{2}dx=\left.\dfrac{1}{2}\dfrac{x^3}{3}\right]_0^2=\dfrac{8}{6}=\dfrac{4}{3}\]
La media de la función de densidad es de \(\dfrac{4}{3}\).
Varianza
Otro valor importante que mide la dispersión de los datos es la varianza. La varianza es, simplemente, el cuadrado de la desviación estándar.
El cálculo es similar al de la función discreta:
\[\text{var}(X)=σ^2=\int_{-\infty}^{+\infty}(x-\mu)^2f(x)dx=\int_{-\infty}^{+\infty}x^2f(x)dx-\mu^2\]
Al igual que la desviación estándar es una medida de dispersión, ambas miden cuánto se desvían los datos del valor esperado.
Calcula la varianza de la función de densidad del ejemplo anterior.
Solución:
Para calcularla aplicamos la fórmula anterior y la media del ejemplo anterior que acabamos de calcular:
\[\text{Var}(X)=\int_{-\infty}^{+\infty}x^2f(x)dx-\mu^2=\int_0^2 x^2\dfrac{x}{2}dx-\dfrac{16}{9}=\dfrac{16}{8}-\dfrac{16}{9}=\dfrac{2}{9}\]
Distribuciones continuas de probabilidad - Puntos clave
- Una función de distribución de probabilidad es una función estadística que nos permite saber todos los posibles resultados de un experimento aleatorio en un rango específico, y la probabilidad de cada uno de estos resultados.
- Para calcular las probabilidades cuando tenemos una variable aleatoria continua, utilizamos lo que se llama la función de densidad.
- La distribución normal es una distribución continua de probabilidad.
- Se conoce como esperanza matemática al producto de la probabilidad de un resultado por el valor esperado.
- Otro valor importante que mide la dispersión de los datos es la varianza; que es, simplemente, el cuadrado de la desviación estándar.
Résumenes 
Exámenes 
Magazine 
Formacion Profesional 
