El arco y su medida
Hay dos definiciones importantes que debes conocer:
El arco de una circunferencia
Un arco es la arista de un sector del círculo, es decir, la arista limitada/delimitada por dos puntos del círculo.
Lalongitud del arco es el tamaño del arco, es decir, la distancia entre los dos puntos delimitadores del círculo.
La medida de un arco
Si consideramos que un arco es la arista entre dos puntos A y B de un círculo, la medida del arco es el tamaño del ángulo entre A, el centro del círculo, y B.
En relación con la longitud del arco, la medida del arco es el tamaño del ángulo que subtiende la longitud del arco.
Aquí tienes una demostración gráfica de estas definiciones:
Hallar la medida de un arco StudySmarter original
Radianes frente a grados
Antes de introducir la fórmula para la medida de un arco, recapitulemos los grados y los radianes.
Para convertir radianes en grados: divide por y multiplica por 180.
Para convertir grados en radianes: divide por 180 y multiplica por.
Éstos son algunos de los ángulos habituales que debes reconocer.
| Grados | 0 | 30 | 45 | 60 | 90 | 120 | 180 | 270 | 360 |
| Radianes | 0 |
Fórmulas de medida y longitud de arco
Hallar la medida del arco con el radio
La fórmula que relaciona la medida del arco (o medida del ángulo) y la longitud del arco es la siguiente:
Donde
- r es el radio del círculo
- es la medida del arco en radianes
- S es la longitud del arco
Podemos hallar la medida del arco dados el radio y la longitud del arco reordenando la fórmula: .
Halla la medida del arco de la circunferencia siguiente en función de su radio, r.
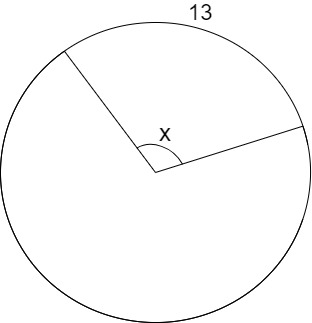
Utilizando la fórmula :
Necesitamos la medida del arco en términos de r, así que tenemos que reordenar esta ecuación:
Hallar la medida del arco con la circunferencia
Si no conocemos el radio r, existe un segundo método para hallar la medida del arco. Si conocemos la circunferencia de un círculo además de la longitud del arco, la relación entre la medida del arco y (o según quieras la medida del arco en grados o radianes) es igual a la relación entre la longitud del arco y la circunferencia.
Donde
c es la circunferencia del círculo
- es la medida del arco en grados
S es la longitud del arco
Halla la longitud de arco, x, del siguiente círculo con una circunferencia de 10 cm.
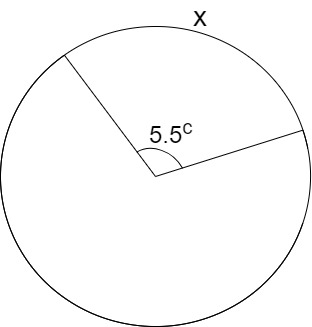
Utilizando la fórmula :
Reordenando, obtenemos
a 3 s.f.
Medidas del arco - Puntos clave
- Un arco es la arista de un sector circular, es decir, la arista delimitada/delimitada por dos puntos del círculo.
- Lalongitud del arco es el tamaño del arco, es decir, la distancia entre los dos puntos delimitadores del círculo.
- La medida del arco es el tamaño del ángulo que subtiende el arco.
- Hallar la medida del arco dados el radio y la longitud del arco:
Donde
r es el radio del círculo.
- es la medida del arco en radianes.
S es la longitud del arco.
Hallar la medida del arco dada la circunferencia y la longitud del arco:
Donde
c es la circunferencia del círculo.
- es la medida del arco en grados.
S es la longitud del arco.
Aprende con 2 tarjetas de Medidas de arcos en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Medidas de arcos
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
