¿Qué es una ecuación diferencial?
Cuando tenemos una ecuación que implica una serie de derivadas, la llamamos ecuación diferencial. Cuando las derivadas son de una función de una variable, la llamamos ecuación diferencial ordinaria (EDO). Cuando hablamos de una ecuación diferencial, solemos hablar de su orden. Por orden se entiende la derivada más alta que está presente en la ecuación. Por ejemplo, la ecuación  es de orden dos, ya que la derivada de mayor orden en la ecuación es de segundo orden.
es de orden dos, ya que la derivada de mayor orden en la ecuación es de segundo orden.
Al resolver una ecuación diferencial, el objetivo es encontrar una función que satisfaga la ecuación. Esta solución no será única, ya que con una derivada se puede añadir una constante que cambie la función pero siga satisfaciendo la ecuación. La única forma de encontrar el valor de esta constante es añadiendo una condición de contorno.
En una ecuación diferencial ordinaria de primer orden, sólo necesitamos una condición de contorno para satisfacer la incógnita. En general, para una ecuación diferencial ordinaria de orden, necesitamos n condiciones de contorno. Una condición de contorno especifica el valor de la función en un punto determinado. Esto te permite calcular el valor de los coeficientes desconocidos.
Verificación de soluciones de ecuaciones diferenciales
Ante una ecuación diferencial, si nos dan una solución potencial, podemos comprobar si es válida o no. Para ello hay que calcular todas las derivadas utilizadas y rellenarlas para ver si la solución potencial es adecuada para satisfacer la ecuación.
Comprueba que  es una solución de
es una solución de  . (Observa aquí que utilizamos para representar
. (Observa aquí que utilizamos para representar  , y para representar
, y para representar  ).
).
Utilizando la Regla del Producto, hallemos la primera y la segunda derivada de y con respecto a x.
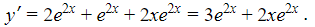
Entonces
Ahora podemos completar los valores para obtener
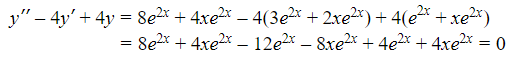
Por tanto, se verifica la solución.
Resolver ecuaciones diferenciales
En el nivel A, sólo necesitamos saber resolver Ecuaciones diferenciales ordinarias separables de primer orden. Separable se refiere al hecho de que las dos variables (normalmente x e y) pueden separarse y luego dividirse para resolverlas.
La forma de una ecuación diferencial separable (para las variables y y x, donde y es una función de x) es  . Podemos reordenarla para obtener
. Podemos reordenarla para obtener , e integrarla para obtener
, e integrarla para obtener . Una vez integrada, ésta es nuestra solución general para la ecuación diferencial. Si es necesario, podemos aplicar condiciones de contorno para encontrar una solución específica.
. Una vez integrada, ésta es nuestra solución general para la ecuación diferencial. Si es necesario, podemos aplicar condiciones de contorno para encontrar una solución específica.
Cabe señalar que, estrictamente hablando, no podemos manipular de esta forma, ya que no es una fracción, sino una Notación para la derivada. Sin embargo, en este caso podemos tratarla como una fracción.
de esta forma, ya que no es una fracción, sino una Notación para la derivada. Sin embargo, en este caso podemos tratarla como una fracción.
Trazar una familia de curvas solución de ecuaciones diferenciales
Cuando buscamos una solución general para una ecuación diferencial, nos quedan constantes en la ecuación general. Estas constantes pueden tener cualquier valor, y seguirían satisfaciendo la ecuación diferencial. La familia de curvas solución es la colección de las Funciones con diversos valores para las constantes.
Encuentra la solución general de  , y dibuja una gráfica que lo muestre con cuatro soluciones particulares diferentes.
, y dibuja una gráfica que lo muestre con cuatro soluciones particulares diferentes.
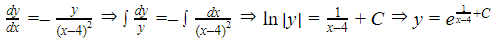
A continuación se muestra una gráfica que muestra cuándo C = -1, 0, 1, 2
 Una familia de soluciones, con C = 2 verde, C = 1 azul, C = 0 rojo y C = -1 morado, Tom Maloy - StudySmarter Originals
Una familia de soluciones, con C = 2 verde, C = 1 azul, C = 0 rojo y C = -1 morado, Tom Maloy - StudySmarter Originals




 es de orden dos, ya que la derivada de mayor orden en la ecuación es de segundo orden.
es de orden dos, ya que la derivada de mayor orden en la ecuación es de segundo orden.  es una solución de
es una solución de  . (Observa aquí que utilizamos para representar
. (Observa aquí que utilizamos para representar  , y para representar
, y para representar  ).
).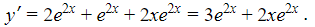
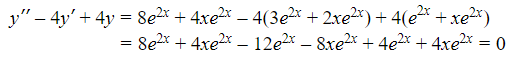
 . Podemos reordenarla para obtener
. Podemos reordenarla para obtener , e integrarla para obtener
, e integrarla para obtener . Una vez integrada, ésta es nuestra solución general para la ecuación diferencial. Si es necesario, podemos aplicar condiciones de contorno para encontrar una solución específica.
. Una vez integrada, ésta es nuestra solución general para la ecuación diferencial. Si es necesario, podemos aplicar condiciones de contorno para encontrar una solución específica. de esta forma, ya que no es una fracción, sino una Notación para la derivada. Sin embargo, en este caso podemos tratarla como una fracción.
de esta forma, ya que no es una fracción, sino una Notación para la derivada. Sin embargo, en este caso podemos tratarla como una fracción. .
. , lo que significa que la solución es de la forma
, lo que significa que la solución es de la forma  . Esto significa que podemos rellenar las dos
. Esto significa que podemos rellenar las dos  . Integrando el lado derecho, obtenemos
. Integrando el lado derecho, obtenemos  . En el lado izquierdo, se trata de una integral estándar, dada como
. En el lado izquierdo, se trata de una integral estándar, dada como  .
. 
 . Observa que aquí hemos combinado ambas constantes en una. Podemos simplificarlo aún más para obtener
. Observa que aquí hemos combinado ambas constantes en una. Podemos simplificarlo aún más para obtener .
. , con
, con .
. .
.  , y el lado derecho se integra en
, y el lado derecho se integra en .
. . Esto puede simplificarse aún más para obtener
. Esto puede simplificarse aún más para obtener .
.  , así que podemos completarlo para obtener
, así que podemos completarlo para obtener .
. .
. , y dibuja una gráfica que lo muestre con cuatro soluciones particulares diferentes.
, y dibuja una gráfica que lo muestre con cuatro soluciones particulares diferentes.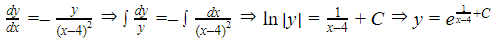

 . El agua sale del depósito a un ritmo proporcional a la raíz cuadrada del volumen del depósito. Halla
. El agua sale del depósito a un ritmo proporcional a la raíz cuadrada del volumen del depósito. Halla  .
.  , lo que significa
, lo que significa .
.  , donde a es una constante de proporcionalidad.
, donde a es una constante de proporcionalidad. .
.  .
. , con solución
, con solución .
.


