Contenidos de aprendizaje
Contenidos de aprendizaje

Descubra los mejores contenidos de aprendizaje para todas las asignaturas.

Resumenes
Asignaturas

Alemán

Alimentación

Antropología

Arqueología

Biología

Chino

Ciencias Ambientales

Ciencias del Deporte

Ciencias Combinadas

Ciencias de la Computación

Ciencias empresariales

Ciencias Políticas

Derecho

Economía

Educación

Enfermería

Español

Estudios de Arquitectura

Estudios de Arte

Estudios de Medios

Física

Francés

Geografía

Historia

Ingeniería

Inglés

Italiano

Literatura

Hostelería y Turismo

Marketing

Matemáticas

Medicina

Psicología

Química

Sociología

Traducción
Funciones
Funciones

Regístrate gratis y descubre todas las funciones de StudySmarter.

Flashcards

StudySmarter AI

Apuntes

Plan de estudios

Sets de estudio

Repeticion espaciada

Exámenes
Qué novedades hay

Flashcards
Aprende y crea tarjetas de estudio como nunca antes.

StudySmarter AI
Todo el material de aprendizaje reunido en un solo lugar.

Apuntes
Crear y editar notas o documentos.

Plan de estudios
Organización perfecta con planes de estudio y listas de tareas.
Recursos
Descubra

Todos los consejos y trucos que necesitas para tus estudios y tu carrera profesional.

Magazine

Hacer carrera

Formacion Profesional

Mobile App
Presentamos

Magazine
Artículos útiles para tus estudios y tu carrera profesional.

Hacer carrera
La mayor oferta de empleo para alumnos y estudiantes.

App móvil
Todo lo que necesitas aprender en una sola aplicación.

Contenidos de aprendizaje

Funciones

Descubra

Reglas del Triángulo

Es posible deducir varias propiedades y valores de triángulos rectángulos utilizando las reglas trigonométricas. Pero, ¿y si se trata de triángulos que no tienen ningún ángulo recto? ¿Podemos seguir aplicando la trigonometría para averiguar diversas propiedades de los triángulos dados, como los ángulos desconocidos, las longitudes o el área?

Pruéablo tú mismo

Contenido verificado
Última actualización: 01.01.1970
Tiempo de lectura: 5 min

Proceso de creación de contenido diseñado por
du contenu vérifiée par
Calidad del contenido comprobada por

Las reglas de los triángulos tratadas en este artículo explorarán esta cuestión con más detalle:

Reglas de los triángulos - regla del seno

La primera regla de triángulos que vamos a tratar se llama regla del seno. La regla del seno puede utilizarse para encontrar los lados o ángulos que faltan en un triángulo.

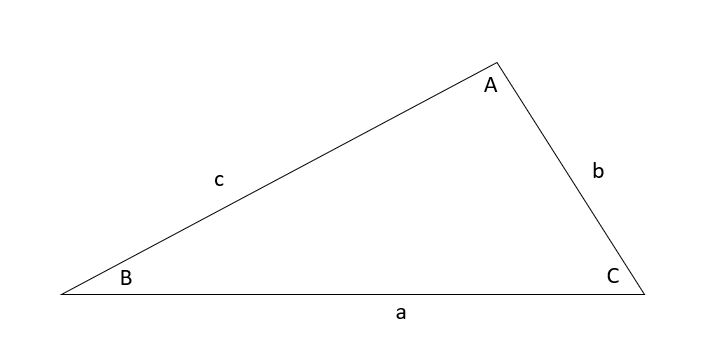
Considera el siguiente triángulo de lados a, b y c, y ángulos, A, B y C.

Regla del seno triangular - StudySmarter

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

Triángulo con lados a, b y c, y ángulos, A, B y C, Nilabhro Datta - StudySmarter Originals

Hay dos versiones de la regla del seno.

Para el triángulo anterior, la primera versión de la regla del seno dice

$\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$

Esta versión de la regla del seno suele utilizarse para hallar la longitud de un lado que falta.

La segunda versión de la regla del seno dice

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$

Esta versión de la regla del seno se suele utilizar para encontrar un ángulo que falta.

Para el siguiente triángulo, halla a.

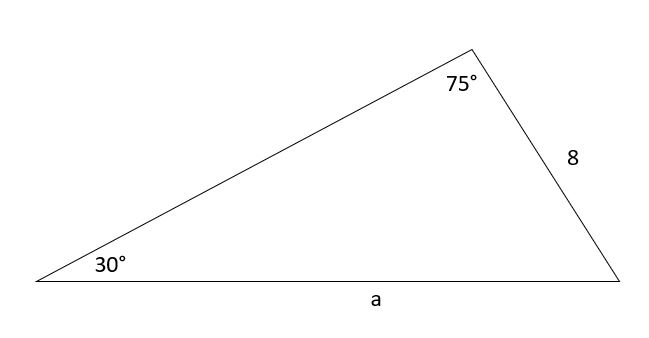
Reglas del triángulo Hallar la longitud de un lado StudySmarter

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

Solución

Según la regla del seno,

$\frac{a}{\sin (A)} = \frac{b}{\sin (B)} \frac{a}{\sin (75)} = \frac{8}{\sin (30)} \frac{a}{0.966} = \frac{8}{0.5} a = 15.455$

Lee Reglas del seno y del coseno para conocer más a fondo la regla del seno.

Para este triángulo, halla x.

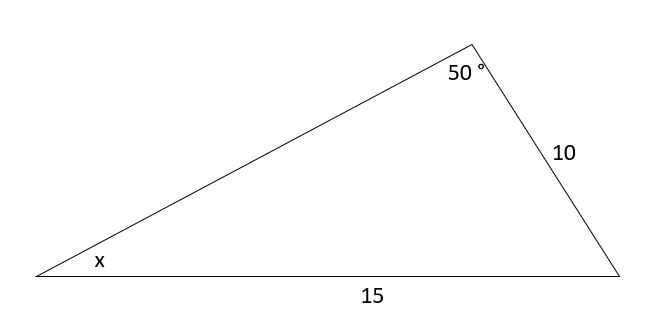
Reglas del triángulo Encontrar un ángulo StudySmarter

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

Solución

Según la regla del seno,

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} \frac{\sin (x)}{10} = \frac{\sin (50)}{15} \frac{\sin (x)}{10} = \frac{0.766}{15} \Rightarrow x = 30.71 °$

Reglas de los triángulos - regla del coseno

La segunda regla de los triángulos que vamos a tratar se llama regla del coseno. La regla del coseno puede utilizarse para encontrar los lados o ángulos que faltan en un triángulo.

Considera el siguiente triángulo con los lados a, b y c, y los ángulos, A, B y C.

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

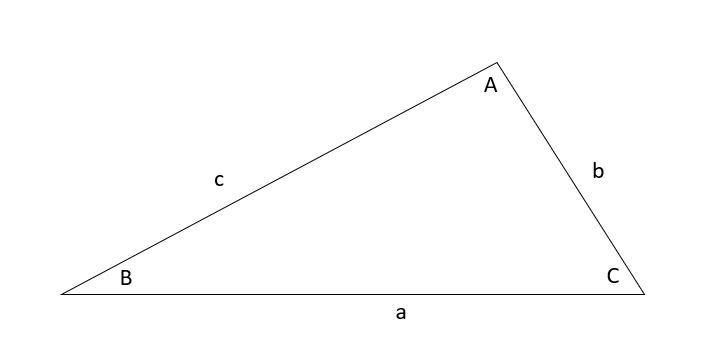
Triángulo con lados a, b y c, y ángulos, A, B y C, Nilabhro Datta - StudySmarter Originals

Existen dos versiones de la regla del coseno.

Para el triángulo anterior, la primera versión de la regla del coseno establece:

a² = b² + c² - 2bc - cos (A)

Esta versión de la regla del coseno suele utilizarse para hallar la longitud de un lado que falta cuando conoces las longitudes de los otros dos lados y el ángulo entre ellos.

La segunda versión de la regla del coseno establece:

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$

Esta versión de la regla del coseno suele utilizarse para hallar un ángulo cuando se conocen las longitudes de los tres lados.

Encuentra x.

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

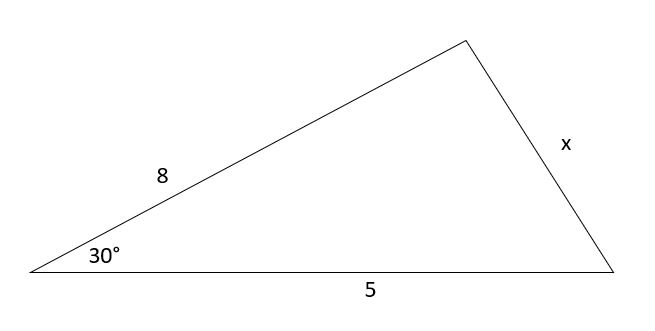
Solución

Según la regla del coseno

a² = b² + c² - 2bc - cos (A)

=> x² = 5² + 8² - 2 x 5 x 8 x cos (30)

=> x² = 19.72

=> x = 4.44

Para el siguiente triángulo, halla el ángulo A.

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

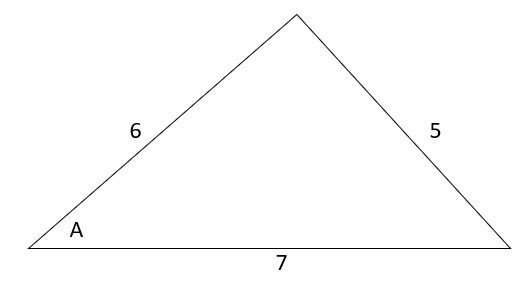
Solución

Según la regla del coseno,

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c} \Rightarrow \cos (A) = \frac{7^{2} + 6^{2} - 5^{2}}{2 \cdot 7 \cdot 6} \Rightarrow \cos (A) = \frac{5}{7} \Rightarrow A = 44.4 °$

Lee Reglas del seno y del coseno para conocer más a fondo la regla del coseno.

Reglas de los triángulos - el área de un triángulo

Ya conocemos la siguiente fórmula:

$A r e a o f a t r i a n g l e = \frac{1}{2} \cdot b a s e \cdot h e i g h t$

Pero, ¿qué ocurre si no conocemos la altura exacta del triángulo? También podemos averiguar el área de un triángulo del que conocemos la longitud de dos lados cualesquiera y el ángulo entre ellos.

Considera el siguiente triángulo:

Reglas de los triángulos área de un triángulo regla del seno StudySmarter

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

El área del triángulo anterior puede hallarse mediante la fórmula:

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

Halla el área del triángulo.

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

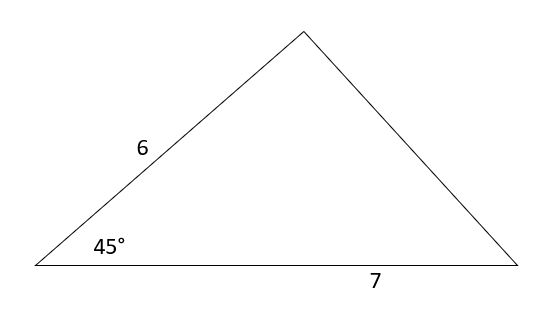
Solución

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} \cdot 6 \cdot 7 \cdot \sin (45) = 14.85$

El área del triángulo es 10 Unidades. Halla el ángulo x.

Quieres ver ésta y muchas más ilustraciones?

Regístrate gratis

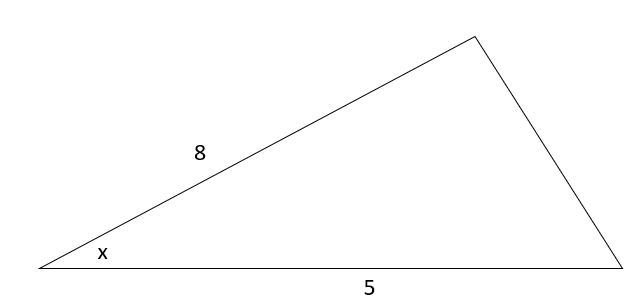
Solución

$A r e a = \frac{1}{2} a b \cdot \sin (C) \Rightarrow 10 = \frac{1}{2} \cdot 5 \cdot 8 \cdot \sin (x) \Rightarrow \sin (x) = 0.5 \Rightarrow x = 30 °$

Haz clic en Área de triángulos para conocer más a fondo la regla del área de triángulos.

Reglas de los triángulos - puntos clave

Puedes utilizar la regla del seno para encontrar los lados o ángulos que faltan en un triángulo.
La primera versión de la regla del seno establece que $\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$ La segunda versión de la regla del seno establece que $\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$
Puedes utilizar la regla del coseno para encontrar los lados o ángulos que faltan en un triángulo.
La primera versión de la regla del coseno afirma que:a² = b² + c² - 2bc - cos (A) La segunda versión de la regla del seno afirma que: $\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$
Podemos averiguar el área de un triángulo del que conocemos la longitud de dos lados cualesquiera y el ángulo entre ellos mediante la siguiente fórmula: $A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Reglas del Triángulo

¿Qué es la regla del triángulo en matemáticas?

La regla del triángulo establece que la suma de las longitudes de dos lados de un triángulo siempre es mayor que la longitud del tercer lado.

¿Cómo se aplica la regla del triángulo?

Para aplicar la regla del triángulo, asegúrate de que la suma de dos lados cualesquiera sea siempre mayor que el tercer lado.

¿Qué asegura la regla del triángulo?

La regla del triángulo asegura que un triángulo puede existir si la suma de las longitudes de dos de sus lados es siempre mayor que el tercer lado.

¿Cómo se llama la desigualdad del triángulo?

Esta regla también es conocida como la desigualdad triangular, una propiedad fundamental en la geometría.

Guardar explicación

¿Cómo te aseguras de que tu contenido sea preciso y confiable?

En StudySmarter, has creado una plataforma de aprendizaje que atiende a millones de estudiantes. Conoce a las personas que trabajan arduamente para ofrecer contenido basado en hechos y garantizar que esté verificado.

Proceso de creación de contenido:

Lily Hulatt es una especialista en contenido digital con más de tres años de experiencia en estrategia de contenido y diseño curricular. Obtuvo su doctorado en Literatura Inglesa en la Universidad de Durham en 2022, enseñó en el Departamento de Estudios Ingleses de la Universidad de Durham y ha contribuido a varias publicaciones. Lily se especializa en Literatura Inglesa, Lengua Inglesa, Historia y Filosofía.

Conoce a Lily

Control de calidad del contenido:

Gabriel Freitas es un ingeniero en inteligencia artificial con una sólida experiencia en desarrollo de software, algoritmos de aprendizaje automático e IA generativa, incluidas aplicaciones de grandes modelos de lenguaje (LLM). Graduado en Ingeniería Eléctrica de la Universidad de São Paulo, actualmente cursa una maestría en Ingeniería Informática en la Universidad de Campinas, especializándose en temas de aprendizaje automático. Gabriel tiene una sólida formación en ingeniería de software y ha trabajado en proyectos que involucran visión por computadora, IA integrada y aplicaciones LLM.

Conoce a Gabriel Gabriel

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más